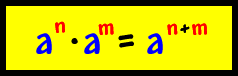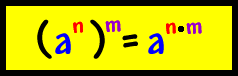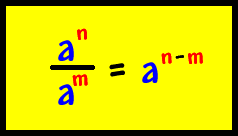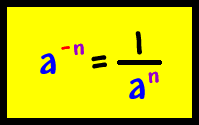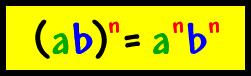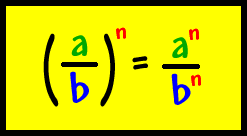|
8.EE.1
8.EE.2 |

8.EE.1 - Exponents and Laws of Exponents - Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 3^2 × 3^–5 = 3^–3 = 1/(3^3) = 1/27.
|
In our first rule, the Product Rule, we see that if you multiple two values with the same base, you add the exponents
This rule, the Power Rule, shows that if you have an "exponent to an exponent" you multiply the two exponents. This rule, called the Quotient Rule, states that if you have two numbers with identical bases and you are dividing them, you subtract the two exponents to get your answer. |
This rule, the Negative Exponent Rule, shows that if you have a base with a negative exponent, yo move the base and the exponent to the bottom of a fraction, make the exponent positive and put a 1 in the numerator.
The Power of a Product rule states that if you have more than one base inside of a parenthesis, you "distribute" the exponent to both of the bases. The Power of a Quotient rule, like the Power of a Product rule, has you "distribute" the exponent to both the bases inside the parenthesis. It is just that this time, you are dividing the two values inside instead of multiplying. |
Video central
|
Here are the two videos from class that we watched. Don't get too excited about the songs!
|
Here are some videos that help to explain the exponent rules that we have covered in class. While these videos do not cover ALL the rules, they do give a quick summary of the rules and how they are done.
|
|
|
|
|