|
What is a Rational Number?
In mathematics, a rational number is any number that can be expressed as the quotient or fraction p/q of two integers. Basically, it means that a rational number can be written as a terminating or as a repeating decimal. For the most part, rational numbers are the numbers that you would be using on a daily basis.
|
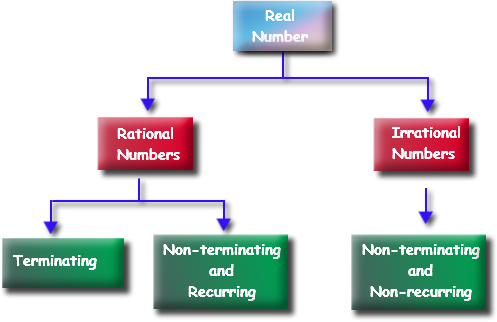
Real Number Flow Chart
As you can see above, all the numbers you can think of can be divided into two categories. If the number terminates (stops) or repeats (same pattern over and over), it is Rational. If the number never stops and never repeats, like the number π or √20, then it is an irrational number.
|
What is an Irrational Number?
In mathematics, an irrational number is any real number that cannot be expressed as a ratio of integers. Informally, this means that an irrational number cannot be represented as a simple fraction. Irrational numbers are those real numbers that cannot be represented as terminating or repeating decimals.
|
Identifying Rational and Irrational Numbers
|
Examples Rational Numbers
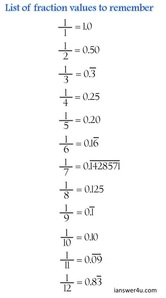
You can see some examples of rational numbers to the right. Every one of these numbers an be written as both a fraction and as a decimal that either stops or has a repeating pattern.
|
Notice the difference in the decimal expansions of the numbers |
Examples of Irrational Numbers

Here are some examples of some irrational numbers. As you can see, they all "go on forever" without repeating. Also notice that every one of the numbers when written in "normal" form needs to have a symbol:
3.14.... needs to use π 2.71828..... needs to use e All the other things need to use the √ symbol, which means square root. |
Converting Repeating Decimals
|
|
Each of these slideshows gives you an example of how to convert a repeating decimal to a fraction.
The one of the left is a "simple" one where you have all the of decimals under the repeating bar. The one on the right shows how to do a problem where not all the numbers are under the repeating fraction bar. |
|
This standard has 4 different components to it. The first part is that you understand the difference between a rational and irrational number. You can see a better explanation of those two terms in the top two videos below. The bottom two videos show a bit more how to compare and convert rational numbers.
These videos, provided by Learnzillion, used to be on Youtube. Learnzillion took them down, but they still have them on their originial website. Below are pictures of the video, and you can simply click on the image to take you to Learnzillion and watch the videos there.
These videos, provided by Learnzillion, used to be on Youtube. Learnzillion took them down, but they still have them on their originial website. Below are pictures of the video, and you can simply click on the image to take you to Learnzillion and watch the videos there.