|
8.G.7 - Application of the PT - Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
|
In the last standard, we focused on how to use the Pythagorean Theorem in order to find the length of a missing side of a right triangle. We also used it to determine if the three sides of the triangle are appropriate length and if they make a right triangle. In this standard, we will be applying the Pythagorean Theorem in order to find the missing sides of shapes that are both two dimensional and three dimensional. In a lot of these problems, the right triangle is "hidden," and in many cases, you may have to spend a few moments to "find it" in order to solve the problem. Additionally, there are many times where you may need to use thePythagorean Theorem more than once in a problem.
CORE UNDERSTANDING - A COUPLE VIDEOS
How to find the missing sides
|
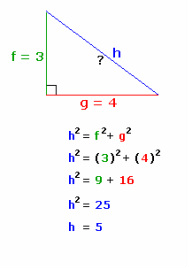
As you can see to the left, you are missing the hypotenuse, the h. To find the hypotenuse, you:
|
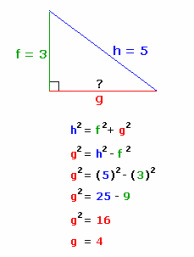
As the example to the left shows, you can also find a missing side. To do this, you do the following:
|
|
Checkup from the neck up
To the right, you can see four example problems.Check the problems above, then compare to the ones to the right. Determine if you are trying to find the hypotenuse or the leg. Think about how you would set up the problem. Once you decide, slide it to the right to see if you would have solved it correctly.
|
|
|
Some Real-World Application Problems
|
|
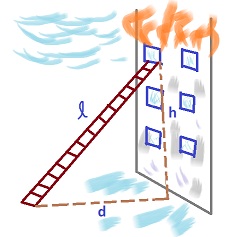
There is a fire on the third story of a building. The height of the third story, as you can see in the picture, would be h. The ladder has a length of l. In order to get the ladder to reach the window where it needs to go, how far away from the building, d, does the ladder need to be?
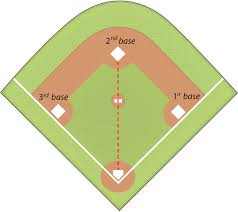
To solve this, you would need to use the Pythagorean Theorem. Using a^2 + b^2 = c^2, we just plug in the correct letters into the problem. So in this case, our new equations would be: d^2 + h^2 = l^2 So if we know the length of the ladder and the length of height of the building, we can just plug in to solve. How long is it from home plate to second based? Well, we would use the Pythagorean Theorem again. If we called the distance from home to first a and the distance from first to second b, we could use the Theorem to find the distance from home to first. That distance would be:
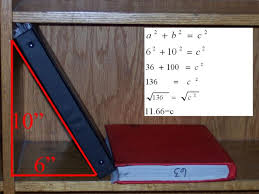
a^2 + b^2 = c^2 We would plug in the a and b, square them, add them together and get c^2. A quick square root would give us our final answer. So depending on the size of the baseball field, we would have different values for the distance from home to second base. Ever have a folder that is too big to fit into a shelf? Have to rest it diagonally? Well, as you can see to the left, this is another application of the Pythagorean Theorem. In this example, you can see the shelf is 10 inches tall, and the folder is going to rest 6 inches away from it.
As the math shows in the example, the use of the Theorem gives use the length of the folder in order to fit this problem scenario. Therefore, the folder could be 11.66 inches tall in order to fit on the shelf with a slight diagonal to it. |
|
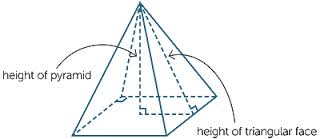
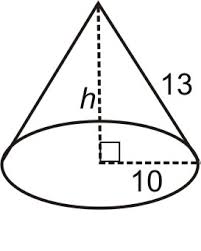
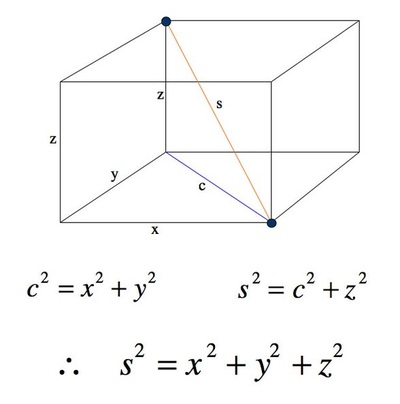
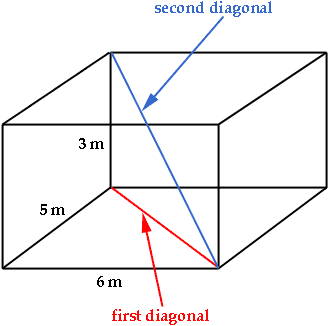
What about 3D Shapes?
In a 3D shape, basically you have a "hidden" Right Triangle where you can use the Pythagorean Theorem in order to find a missing side. Check out the video to the right, and then think about the problems that we see below and how to use the Pythagorean Theorem in order to solve them.
|
Many 3D shapes actually will require you use the PT more than once in order to solve.
In my class, rounding answers are ok. Just round to 2 decimal points.
|
|
|
|
When given a 3D shape, as you see to the left, you need to find the "hidden" right triangle in them. Here's what to look for:
|