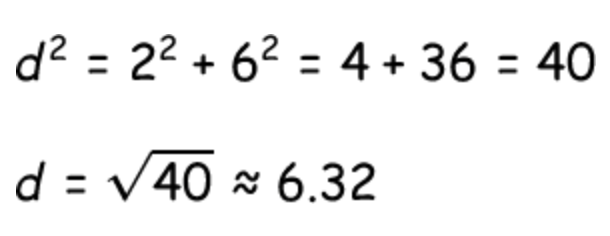|
8.G.8 - Pythagorean Theorem and Coordinates - Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.
|
|
Core Concepts Videos
|
|
The Steps
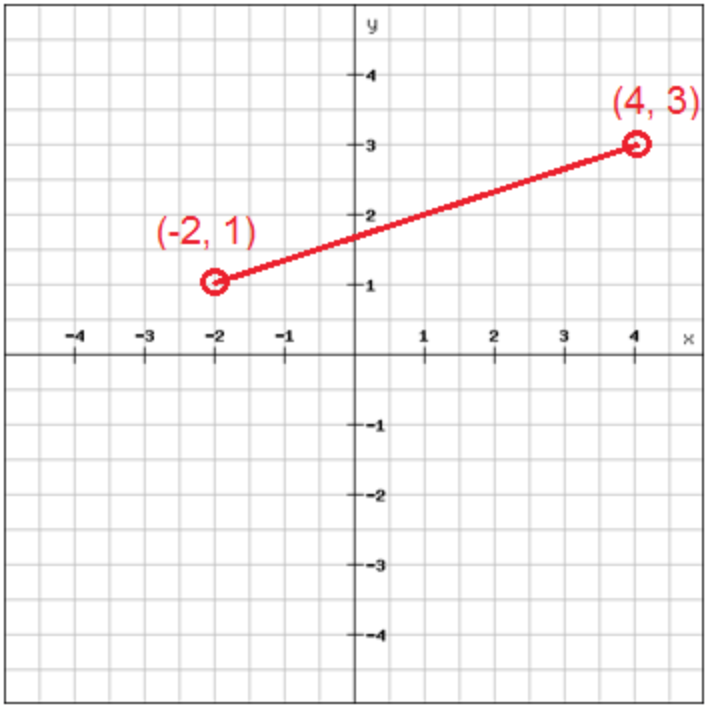
First, you are given 2 points on a coordinate plane. You need to then count how far it is horizontally and vertically between the two points. You can see that below.
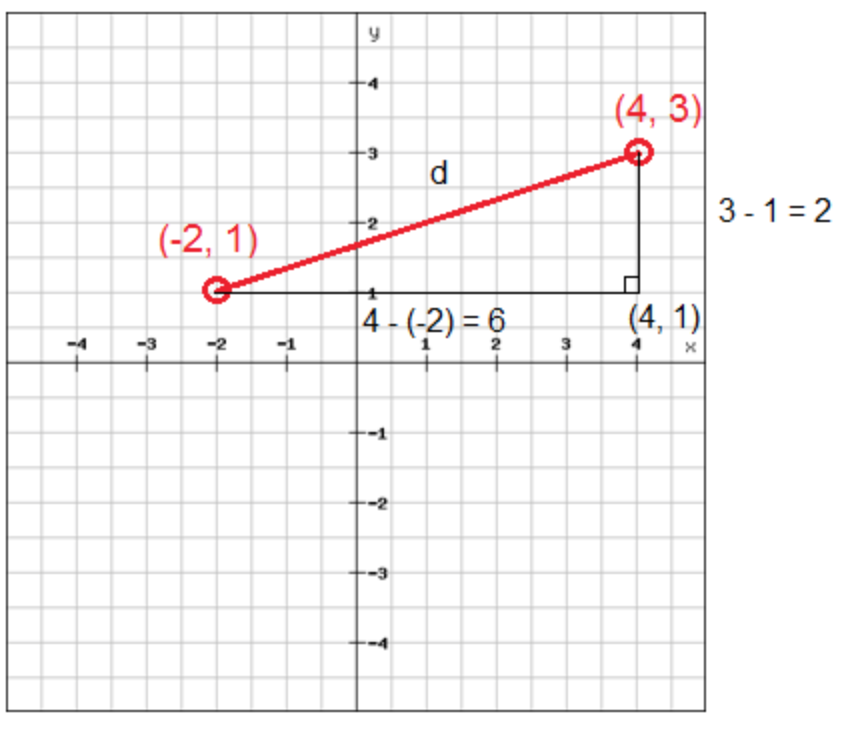
Once you count the horizontal and vertical distance, as you see above, you then place the values into the legs of the Pythagorean Theorem, as you can see below.
|
If you check back with standard 8.EE.5 and 8.EE.6, you will remember that we could find the slope and the unit rate of a line on a coordinate plane. Well, in this standard, we just continue this concept and realize that to find the distance between two points, we need to use the same values we use for slope and plug them into the Pythagorean Theorem.
______________________________ This video continues on with the concepts of finding the distance between two points on the coordinate plane. Finding the distance between two points horizontally or vertically is easy, and this shows you how to combine in the "diagonal" lines using the concepts of slope and the Pythagorean Theorem. So for this shape you see, you have to use the Pythagorean Theorem once and add it to the other 3 sides.
______________________________ In this final video here, you can se how you would go about finding the area of a shape on the coordinate plane using the Pythagorean Theorem. First, determine what shape you are working with and what sides you need to use for the area formula. Then you can find those sides using the Pythagorean Theorem, if needed, and use those in the area formula to find the area.
|
Finding the distance.....
Finding the perimeter.....
Finding the area.....
|